ADH's Blog！

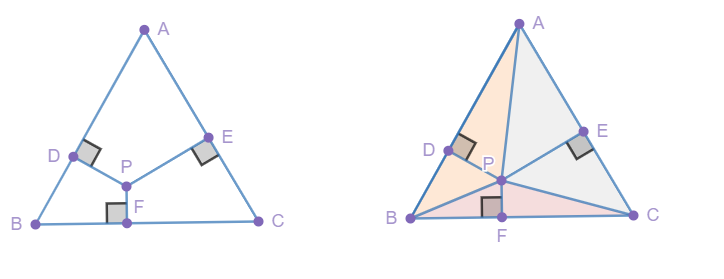
$\Huge\textsf{维维亚尼定理}$

在等边三角形内任意一点P跟三边的垂直距离之和，等于三角形的高。

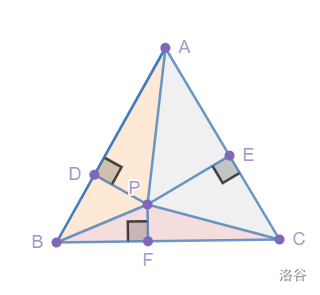
证明太简单了：

设这个等边三角形为$\triangle ABC$，P到三边的三个垂足为$D,E,F$

连接$AP,\;BP,\;CP$

则$S_{\triangle ABC}=S_{\triangle APB}+S_{\triangle BPC}+S_{\triangle CPA}$

$=\frac{1}{2}AB*PD+\frac{1}{2}AC*PE+\frac{1}{2}BC*PF$

$=\frac{1}{2}*AB*(PD+PE+PF)$

又$\because S_{\triangle ABC}=\frac{1}{2}* AB\; *$ 高

$\therefore \frac{1}{2}*AB*(PD+PE+PF) = \frac{1}{2}* AB\; *$ 高

即$PD+PE+PF\;$ = 高。

适用范围：未知，从来没用过。

转载请注明出处 $\tiny\textbf{（虽然应该不会有人来抄我这个小菜鸡的文章XD）}$