《平几纲目》553题
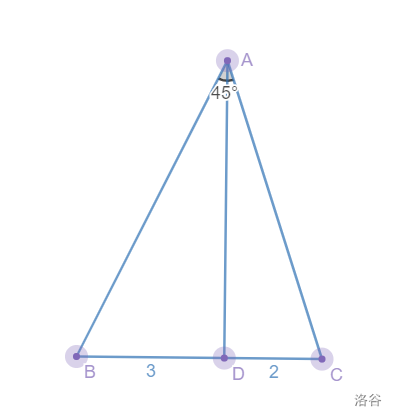
如图,△ABC中,BD=3, CD=2, AD⊥BC, ∠BAC=45°,求AD.
想必大家不一会儿就能算出结果。
但终点不在此:
此题有
39种解法
江湖人称:万 法 归 宗,醍 醐 灌 顶
我这个小菜鸡只做出了8种做法,是最好想出来的几种,在此与大家分享。
法<1>
因为不用辅助线所以没有图。
设AD=x,勾股定理得AB=x2+9, AC=x2+4
由于三角形面积等于两边乘积乘上夹角的正弦值的一半
也等于底乘高的一半
就可以列出方程:21x2+9×x2+4×sin45°=2(3+2)x
解得x1=6,x2=1.
但是x=1很明显是取不到的,可以通过余弦定理算出∠BAC=135°.
∴AD=6.
那为什么会有x=1这个结果呢?
我们在小学二年级就学过诱导公式,可以得知 sin 135°= sin 45 °
也就是说,在乘上sin 45°时等同于乘上 sin 135°
所以会有这个结果
“小学二年级”是毕导的梗啦,快来素质三连
法<2>
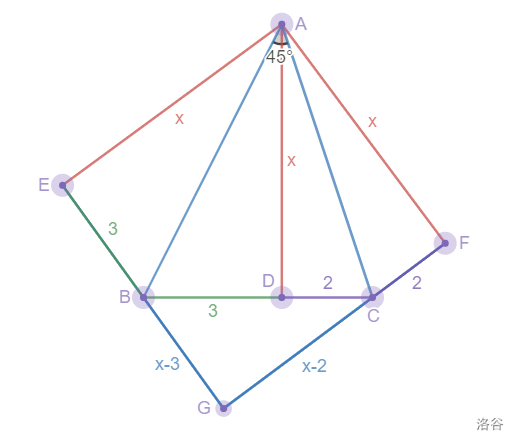
将△ABD沿AB翻折至△ABE,将△ACD沿AC翻折至△ACF,
延长EB、FC交于点G
则BE=BD=3,CF=CD=2,AE=AF=AD,∠EAF=2∠BAC=90°
易得四边形AEGF为正方形
设AD=x,则AE=AF=EG=FG=x,BG=EG−EB=x−3,CG=FG−FC=x−2
勾股定理得BC2=BG2+CG2,∴(x−3)2+(x−2)2=52
解得x=6,即AD=6.
法<3>
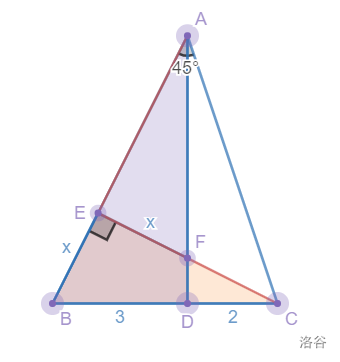
作CE⊥AB于E交AD于F
则△AEC为等腰直角三角形
易得△AEF≅△CEB(AAS或ASA)
∴AF=BC=5,BE=EF
之后有两种思路:
(1)连接BF、CF,用法1的思路得出FD=1,则AD=AF+FD=5+1=6.
其实△BFC就是法1中算出AD=1时三角形的样子
(2)设BE=EF=x
勾股定理得AE=EC=BC2−EB2=25−x2
∴FC=EC−EF=25−x2−x
易得△EBC∼△DFC(AA)
∴BCEC=FCDC
即525−x2=25−x2−x2
解得x1=5,x2=2310(相信我,能解开的)
由于直角三角形斜边大于直角边,舍去x2,∴x=5.
易得AD=6.
法<4>
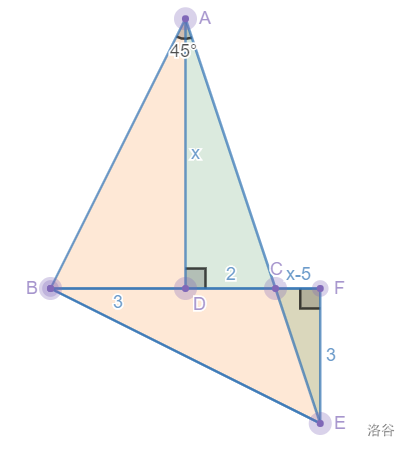
法<5>
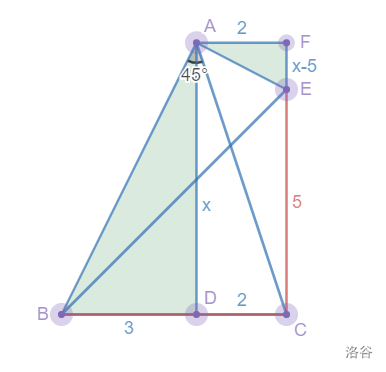
法<6>

法<7>
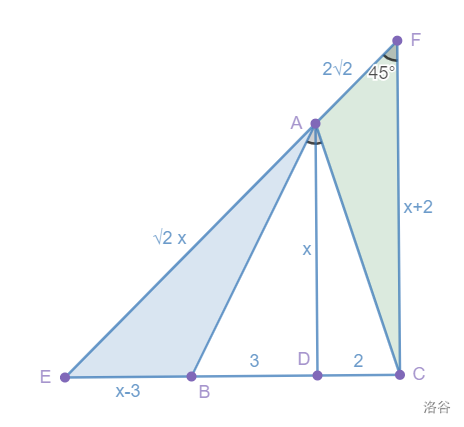
法<8>

未完